Voices from the Sylff Community

Network analysis has emerged as a key technique in many fields of study, including economics, geography, history, and sociology. One fundamental concept that researchers try to capture is centrality: a quantitative measure revealing the importance of nodes in the network. The values assigned to the nodes are expected to provide a ranking which identifies the most important vertices. Naturally, the word “importance” has a wide range of meanings, leading to many different definitions of centrality. László Csató, a Sylff fellow at Corvinus University of Budapest in Hungary, is exploring the methodological background of some centrality indices.

* * *

In the analysis of complex social and economic structures, actors and the relationships among them are often interpreted as a network. The topology of the network can provide insight into its characteristics and functioning independently from the chosen system (a group of people, a supply chain, international trade relations). The graph-theoretical approach offers a possible approach to modelling these networks. Its strengths lie in the measurement of structural attributes as well as in visualization.

A well-known concept of the graph-theoretic analysis is centrality, which reflects the relative importance of the nodes in the whole network. Many methods exist for this purpose, although not every metric is suitable for every network – the choice depends on the nature of processes in the network and the aims of the analysis.

Most centrality measures have an interpretation on the network graph. However, their axiomatic background deserves more attention: little is known about which measures are excluded and which are supported by accepting a plausible property. The adopted approach is a standard path in (cooperative) game and social choice theory, and is gradually coming to prominence in economics, illustrated by the Nobel Memorial Prize in Economic Sciences awarded to Alvin E. Roth and Lloyd S. Shapley in 2012. It can significantly contribute to the effort to find the right measures for a network.

Since my research has a strong theoretical orientation, I want to illustrate it through an example. Readers interested in the details can consult two working papers by me on the topic.^1,2

This paper attempts to develop an index for measuring the accessibility of nodes in networks where each link has a value such that a smaller number is preferred. Examples might include distance, cost, or travel time. In the following, we will give some insight into the results.

Measuring Accessibility

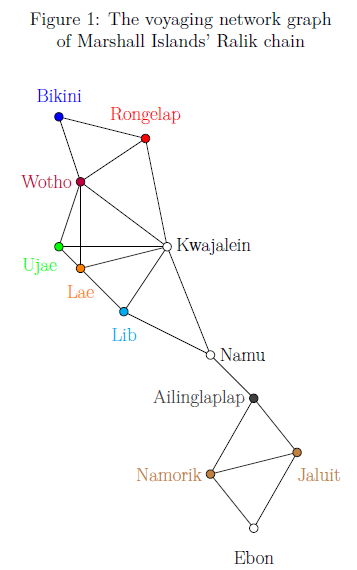
The Marshall Islands in eastern Micronesia are divided into two atoll chains, one of which is Ralik. Figure 1 shows a (simplified) graph of the voyaging network among the 12 islands of the Ralik chain (Ailinglaplap, Bikini, Ebon, Jaluit, Kwajalein, Lae, Lib, Namorik, Namu, Rongelap, Ujae, Wotho). The links between the nodes show the possible routes of inter-island journeys by canoe. For example, it is not feasible to directly travel from Bikini to Jaluit: this journey requires at least five inter-island hops through Rongelap, Kwajalein, Namu and Ailinglaplap. We can therefore say that the distance between Bikini and Jaluit is 5. The problem is to provide a numerical answer to the question “How accessible is a node from other nodes in the Ralik chain?” The islands should be ranked with respect to the probability that they might become the centre of the chain.

An obvious solution is distance sum, the sum of the distances to all the other nodes. For example, Ailinglaplap has a distance sum of 25 since its distance to Bikini is 4, to Ebon 2, to Jaluit 1, and so on. The distance sum is characterized by three independent properties (axioms) such that it satisfies all of them, but any other accessibility index violates at least one property. The three conditions are as follows:

• Anonymity: The accessibility ranking does not depend on the name of the nodes. Note that Jaluit and Namorik are structurally equivalent in the network, both being connected only to Ailinglaplap and Ebon.
• Independence of distance distribution: If the distance of a node is decreased and the distance of another node is increased by the same amount, the accessibility ranking does not change.
• Dominance preservation: A node not far from any other is at least as accessible. For instance, Rongelap should be more accessible than Bikini since the former is closer to certain nodes (e.g., Kwajalein), and there does not exist any island which is farther from Rongelap than from Bikini.

The distance sum focuses exclusively on the shortest paths. Sometimes this is not a desirable feature, as these paths can be vulnerable to link disruptions. Therefore a generalized distance sum, a parametric family of accessibility indices, is suggested. It is linear (easy to calculate), considers the accessibility of vertices besides their distances, and depends on a parameter in order to control its deviation from distance sum. This means that it should violate one axiom of the characterization above, which turns out to be the independence of distance distribution. However, the generalized distance sum is anonymous and satisfies dominance preservation if its parameter meets an appropriate condition.

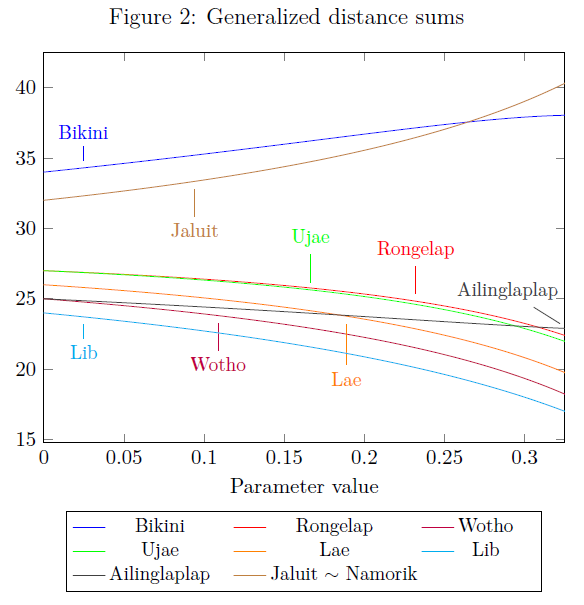
Figure 2 shows the generalized distance sums for some nodes (on the vertical axis) as a function of a parameter (on the horizontal axis), which measures the influence of the other (i.e., not the shortest) paths. If the parameter is zero, the generalized distance sum is equal to the distance sum, however, some changes can be observed by increasing the value of the parameter:

• The tie between Ailinglaplap and Wotho (25) is broken for Wotho. This makes sense since the nodes around Wotho have more links among them.
• The tie between Rongelap and Ujae (27) is broken for Ujae. This is justified by Ujae's direct connection to Lae instead of Bikini as the former is more accessible than the latter.
• Lae (26), Rongelap, and Ujau gradually overtake Ailinglaplap (25) and Bikini (34) overtakes Jaluit and Namorik (32) in the accessibility ranking. The reason is that the network has essentially two components: the link between Ailinglaplap and Namu is a cut-edge, and the above part around Kwajalein (where Lae, Rongelap, Ujae, and Bikini are located) is bigger and has more internal links.

Kwajalein (with a distance sum of 20) and Namu (21) are the first and second nodes in the accessibility ranking for any value of the parameter. Ebon (34) is “obviously” the least accessible node. These nodes are not shown in Figure 2.

To summarize, the generalized distance sum seems to reflect the vulnerability of accessibility to a disruption on the edge between Ailinglaplap and Namu: if this occurs, then the islands of Ailinglaplap, Ebon, Jaluit, and Namorik suffer more as they have a smaller “internal” network. The parameter can be said to measure this danger to a certain extent.

What Is It Good For?

Accessibility measures can be used in a number of interesting ways:

• Knowledge of which nodes have the highest accessibility could be of interest in itself (e.g., by revealing their strategic importance);
• The accessibility of vertices could be statistically correlated to other economic, sociological, or political variables;
• Accessibility of the same nodes (e.g., urban centers) in different networks (e.g., transportation, infrastructure) could be compared;
• Proposed changes in a network could be evaluated in terms of their effect on the accessibility of vertices;
• Networks (e.g., empires) could be compared by their propensity to disintegrate. For example, it may be difficult to manage from a unique center if the most accessible nodes are far from each other.

Network analysis has emerged as a key technique in modern sociology as well as in anthropology, biology, economics, geography, history, and political science. My methodological research aspires to support these applications to get an insight into different networks. I believe robust mathematical foundations are crucial to a better understanding of similar complex systems.

¹Csató, L. (2015): Measuring centrality by a generalization of degree. Corvinus Economics Working Papers 2/2015. URL: http://unipub.lib.uni-corvinus.hu/1846/ This paper contributes to network analysis, dealing with the issue of how to identify key nodes in a network. For this purpose a new centrality measure, called the generalized degree, is suggested, based on the idea that a link to a more interconnected node is preferable to a connection to a less central one.
²Csató, L. (2015): Distance-based accessibility indices. Corvinus Economics Working Papers 12/2015.URL: http://unipub.lib.uni-corvinus.hu/1986/